A (fellow student) friend of mine once told me that there had been no such demarcation line between "the Sciences" and "the Arts" in a history not so far from the present and there is no scope of denying any of that.Not to mention ALL Mathematicians were philosophers first (great or not depends upon an individual's cognitive ability and that again depends on genetics and hormones).Physics joined hands with logic and the entire programming concept was born because of Metaphysics.There was imagination before innovation,at least 'the before' we all are capable of understanding.
A lot has been going through my mind these days.Out of several terrible attributes I possess,one is multi-faceted eagerness.I love reading everything and watching it all from Statistics,Political Science to Epidemiology and Astrophysics.
And I was confused in the worst manner when going through the phase of decision making on what to study.I decided Economics and Economics only (not sure what stream but something like welfare or heterodox will serve me best and let me serve best) because it was not a single stream and a reason I usually do not disclose.....I did not want to let go of writing or speaking,communications have always been natural to me.
Now,Economics is a culmination of many,several subjects including psychology,history,sociology,maths,statistics,literature,political science,logic,engineering,marketing,finance and what not! Well,I also believe I fight the hardest when emotionally unwell and it is not too stark a condition and I am at the least able to clearly think things.Also, for a few weeks,I have been muttering "set theory works like this" in programming classes and "De Morgan's laws also work for programming" in Maths classes.I do not sadly have Philosophy in my combination but I am regular at studying all of the Social Sciences and literature,at least English literature,so I am confidant that I am not illiterate in any of these fields.
A few days ago,while on a debate on Gandhi,someone from the other end came up with Epistemology and it got me so finely encouraged about Boolean Algebra! There is a concept called 'dualism' in Epistemology and it works with psychology,namely cognitive psychology and without learning dualism,you do not know how to differentiate between Boolean variables and real numbers.This also reminded me of "tends to"(since none of the sources of knowledge was supposed to make you fundamental in dualism,you had to draw conclusion from each of these facts,and that was not absolute),something which is used in Limit,broadly Calculus.Stringing up all these and a broad section of philosophy I have been consumed in the last few days,I can't help but share it (mostly nobody here understand these things much and I don't think they think an alphabet more than individual economical well being ; as if education is a commodity,you digest it and sell it to corporations that can pay you just to afford luxuries.) It is weird that researchers and scientists earn much less than engineers/analysts working in the corporations but I think the passion is all that matters and all that lives,somewhat beyond our fish-eyed,minimal vision.
I,however am going cynical about this connectivity.Even 'Brotherhood' (Octavio Paz) reminded me of individualism and the economy and existentialism and dialectics and Marxism and naturalism and physiocrats and Adam Smith and when asked to explain the poem in the class,I coughed up how it was more on existentialism (mis-spelt extentialism here) than on the insignificance of human beings.I do not think anyone understood that though but it again got me drawn into my Economics book for the next two hours instead of being able to concentrate on English class.Sighs.So,now the professional part.
Content of this article shows links between Set Theory,Boolean Algebra,Logic,Cognitive Psychology and Epistemology in particular.
I am sure you need to know the littlest concept of Set Theory before you go through this article but if anyone wants reference,I have provided it here.This definition has been COLLECTED from Stanford Encyclopedia of PHILOSOPHY. ;)
Set theory is the mathematical theory of well-determined collections, called sets, of objects that are called members, or elements, of the set. Pure set theory deals exclusively with sets, so the only sets under consideration are those whose members are also sets.
The theory of the hereditarily-finite sets, namely those finite sets whose elements are also finite sets, the elements of which are also finite, and so on, is formally equivalent to arithmetic. So, the essence of set theory is the study of infinite sets, and therefore it can be defined as the mathematical theory of the actual—as opposed to potential—infinite.
The concept of a set appears deceivingly simple, at least to the trained mathematician, and to such an extent that it becomes difficult to judge and appreciate correctly the contributions of the pioneers. What cost them much effort to produce, and took the mathematical community considerable time to accept, may seem to us rather self-explanatory or even trivial.
Three historical misconceptions that are widespread in the literature should be noted at the outset: (1) It is not the case that actual infinity was universally rejected before Cantor.
(2) Set-theoretic views did not arise exclusively from analysis, but emerged also in algebra, number theory, and geometry.
(3) In fact, the rise of set-theoretic mathematics preceded Cantor's crucial contributions. All of these points shall become clear in what follows.
The notion of a collection is as old as counting, and logical ideas about classes have existed since at least the “tree of Porphyry” (3rd century C.E.). Thus it becomes difficult to sort out the origins of the concept of set. But sets are neither collections in the everyday sense of this word, nor “classes” in the sense of logicians before the mid-19th century. Ernst Zermelo, a crucial figure in our story, said that the theory had historically been “created by Cantor and Dedekind”. This suggests a good pragmatic criterion: one should start from authors who have significantly influenced the conceptions of Cantor, Dedekind, and Zermelo. For the most part, this is the criterion adopted here. Nevertheless, as every rule calls for an exception, the case of Bolzano is important and instructive, even though Bolzano did not significantly influence later writers.
In 19th century German-speaking areas, there were some intellectual tendencies that promoted the acceptance of the actual infinite (e.g., a revival of Leibniz's thought). In spite of Gauss's warning that the infinite can only be a manner of speaking, some minor figures and three major ones (Bolzano, Riemann, Dedekind) preceded Cantor in fully accepting the actual infinite in mathematics. Those three authors were active in promoting a set-theoretic formulation of mathematical ideas, with Dedekind's contribution in a good number of classic writings (1871, 1872, 1876/77, 1888) being of central importance.
Now,let us find out how Set Theory links to Boolean Algebra. There is a very nice documentation available from one of the hosted pdf documents from University of Western Australia.You could click on the third link in the bibliography to have a read.It is basic but very descriptive and is recommended.


Bibliography
A lot has been going through my mind these days.Out of several terrible attributes I possess,one is multi-faceted eagerness.I love reading everything and watching it all from Statistics,Political Science to Epidemiology and Astrophysics.
And I was confused in the worst manner when going through the phase of decision making on what to study.I decided Economics and Economics only (not sure what stream but something like welfare or heterodox will serve me best and let me serve best) because it was not a single stream and a reason I usually do not disclose.....I did not want to let go of writing or speaking,communications have always been natural to me.
Now,Economics is a culmination of many,several subjects including psychology,history,sociology,maths,statistics,literature,political science,logic,engineering,marketing,finance and what not! Well,I also believe I fight the hardest when emotionally unwell and it is not too stark a condition and I am at the least able to clearly think things.Also, for a few weeks,I have been muttering "set theory works like this" in programming classes and "De Morgan's laws also work for programming" in Maths classes.I do not sadly have Philosophy in my combination but I am regular at studying all of the Social Sciences and literature,at least English literature,so I am confidant that I am not illiterate in any of these fields.
A few days ago,while on a debate on Gandhi,someone from the other end came up with Epistemology and it got me so finely encouraged about Boolean Algebra! There is a concept called 'dualism' in Epistemology and it works with psychology,namely cognitive psychology and without learning dualism,you do not know how to differentiate between Boolean variables and real numbers.This also reminded me of "tends to"(since none of the sources of knowledge was supposed to make you fundamental in dualism,you had to draw conclusion from each of these facts,and that was not absolute),something which is used in Limit,broadly Calculus.Stringing up all these and a broad section of philosophy I have been consumed in the last few days,I can't help but share it (mostly nobody here understand these things much and I don't think they think an alphabet more than individual economical well being ; as if education is a commodity,you digest it and sell it to corporations that can pay you just to afford luxuries.) It is weird that researchers and scientists earn much less than engineers/analysts working in the corporations but I think the passion is all that matters and all that lives,somewhat beyond our fish-eyed,minimal vision.
I,however am going cynical about this connectivity.Even 'Brotherhood' (Octavio Paz) reminded me of individualism and the economy and existentialism and dialectics and Marxism and naturalism and physiocrats and Adam Smith and when asked to explain the poem in the class,I coughed up how it was more on existentialism (mis-spelt extentialism here) than on the insignificance of human beings.I do not think anyone understood that though but it again got me drawn into my Economics book for the next two hours instead of being able to concentrate on English class.Sighs.So,now the professional part.
Content of this article shows links between Set Theory,Boolean Algebra,Logic,Cognitive Psychology and Epistemology in particular.
I am sure you need to know the littlest concept of Set Theory before you go through this article but if anyone wants reference,I have provided it here.This definition has been COLLECTED from Stanford Encyclopedia of PHILOSOPHY. ;)
Set theory is the mathematical theory of well-determined collections, called sets, of objects that are called members, or elements, of the set. Pure set theory deals exclusively with sets, so the only sets under consideration are those whose members are also sets.
The theory of the hereditarily-finite sets, namely those finite sets whose elements are also finite sets, the elements of which are also finite, and so on, is formally equivalent to arithmetic. So, the essence of set theory is the study of infinite sets, and therefore it can be defined as the mathematical theory of the actual—as opposed to potential—infinite.
The concept of a set appears deceivingly simple, at least to the trained mathematician, and to such an extent that it becomes difficult to judge and appreciate correctly the contributions of the pioneers. What cost them much effort to produce, and took the mathematical community considerable time to accept, may seem to us rather self-explanatory or even trivial.
Three historical misconceptions that are widespread in the literature should be noted at the outset: (1) It is not the case that actual infinity was universally rejected before Cantor.
(2) Set-theoretic views did not arise exclusively from analysis, but emerged also in algebra, number theory, and geometry.
(3) In fact, the rise of set-theoretic mathematics preceded Cantor's crucial contributions. All of these points shall become clear in what follows.
The notion of a collection is as old as counting, and logical ideas about classes have existed since at least the “tree of Porphyry” (3rd century C.E.). Thus it becomes difficult to sort out the origins of the concept of set. But sets are neither collections in the everyday sense of this word, nor “classes” in the sense of logicians before the mid-19th century. Ernst Zermelo, a crucial figure in our story, said that the theory had historically been “created by Cantor and Dedekind”. This suggests a good pragmatic criterion: one should start from authors who have significantly influenced the conceptions of Cantor, Dedekind, and Zermelo. For the most part, this is the criterion adopted here. Nevertheless, as every rule calls for an exception, the case of Bolzano is important and instructive, even though Bolzano did not significantly influence later writers.
In 19th century German-speaking areas, there were some intellectual tendencies that promoted the acceptance of the actual infinite (e.g., a revival of Leibniz's thought). In spite of Gauss's warning that the infinite can only be a manner of speaking, some minor figures and three major ones (Bolzano, Riemann, Dedekind) preceded Cantor in fully accepting the actual infinite in mathematics. Those three authors were active in promoting a set-theoretic formulation of mathematical ideas, with Dedekind's contribution in a good number of classic writings (1871, 1872, 1876/77, 1888) being of central importance.
Now,let us find out how Set Theory links to Boolean Algebra. There is a very nice documentation available from one of the hosted pdf documents from University of Western Australia.You could click on the third link in the bibliography to have a read.It is basic but very descriptive and is recommended.
The article further claims these propositions : -
The rules of Logic that we have seen in the previous two sections underpin the propositions of
mathematics. We will define a proposition to be a statement that can be demonstrated to be
true, (and by true we mean: for all instances of the statement it is true). In this context, it is
customary to use ‘=⇒’ rather than ‘→’, and ‘⇐⇒’ rather than ‘↔’.
9 PROPOSITIONS 6
Thus, if P and Q are statements then
P =⇒ Q
means: P implies Q, i.e. that whenever P is true then Q must also be true. There are several
other ways of saying this; simplest is just “If P then Q”. One can also say: “P only if Q”; or
switch them around and say: “Q if P” (symbolically: Q ⇐= P); or that: “P is a sufficient
condition for Q”; or that: “Q is a necessary condition for P”. For example, if A is the
statement “n is a prime” and B is the statement “n is a natural number” then A =⇒ B is a
proposition.
Also, ¬P is the negation of P, e.g. if A is the statement “n is a prime” then ¬A would
mean “n is not a prime.”
Finally, if P =⇒ Q and Q =⇒ P we write: ‘P ⇐⇒ Q’ or ‘P if and only if Q’.
Observe how this is made up of ‘P if Q’ (P ⇐= Q) and ‘P only if Q’ (P =⇒ Q). We can
also say P is a necessary and sufficient condition for Q. A shorthand way of writing “if
and only if” is the odd-looking word if.
The sort of propositions that are important in mathematics are theorems, corollaries
(singular: corollary) and lemmas. Theorems are the most important: everybody knows
about Pythagoras’ Theorem. In this course, (and in other advanced mathematics) a theorem
appears in two parts. The first is a statement of the theorem, with some sort of label like
“Theorem 5” or “Lagrange’s Theorem”. The second part is the proof of the theorem which
begins with the word “Proof” and ends with the symbol . Lemmas are (usually short, easy)
propositions that are used to prove theorems; corollaries are propositions that follow easily
from theorems.
Also,you can clearly 'discover' a few things except for compliment.Such as, to OR means to add (also applies in Probability). To 'AND' means to multiply and there is one dualism principle working here. For example,the two distributive properties of set theory work if you try to apply it in Boolean Algebra.
That is,say, we have to prove A + BC = (A + B)(A + C) in Boolean Algebra.
R.H.S = (A + B)(A + C) = AA + AC + AB + BC = A(1 + C) + AB + BC = A + AB + BC = A(1 + B) + BC = A + BC = L.H.S
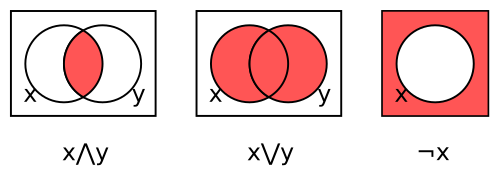
This is exactly the same thing you can use Venn diagrams or logical statements to prove in Set Theory.

Venn diagrams for conjunction, disjunction, and complement
About the dualism attribute,if you replace addition with multiplication or vice versa,you will get a completely new monotone law that fits the relation.Now,in case of set theory,which evolved from insight into the study of the philosophy of geometry,primarily.Now,before I am attacked with the notion that Cantor started out with binomial theorem and that every real roots of the equation are of the form an xn + an-1 xn-1 + an-2 xn-2 + . . . + a1 x + a0 = 0, we are talking about the influence he started from.
Bernhard Riemann proposed visionary ideas about topology, and about basing all of mathematics on the notion of set or “manifold” in the sense of class (Mannigfaltigkeit), in his celebrated inaugural lecture “On the Hypotheses which lie at the Foundations of Geometry” (1854/1868). Also characteristic of Riemann was a great emphasis on conceptual mathematics, particularly visible in his approach to complex analysis (which again went deep into topology). To give but the simplest example, Riemann was an enthusiastic follower of Dirichlet's idea that a function has to be conceived as an arbitrary injective correspondence between numerical values, be it representable by a formula or not; this meant leaving behind the times when a function was defined to be an analytic expression. Through this new style of mathematics, and through his vision of a new role for sets and a full program for developing topology, Riemann was a crucial influence on both Dedekind and Cantor.
This proves that this was more about the philosophy that they started with.Cantor is credited,solely credited with the invention of 'Set Theory',something that was absolutely workable but abstract at its origin. But this is how modern electronic devices work. So,to talk about problem solving and perception,both of which are elements of cognitive psychology.(Ref. "Mathematics is a set of rather specialised habits of behaviour towards certain sorts of qualities and relations." Thorndike,1922)And this still links to Metaphysics,no one for sure knows where lies the origin! In fact,Lady Ada,the first known programmer who was also a friend of Charles Babbage and someone who was really interested about the analytical engine,described her approach as "poetical science" and herself as an "Analyst (& Metaphysician)".
George Boole,again,while finding the relations of addition in logic,referred to the concept of algebra of sets and abstract algebra.
A core feature of abstract algebra is the existence of domains where familiar laws fail to hold. A striking example is commutativity of multiplication, which as we noted in the introduction need not hold for the multiplication of an arbitrary group, even so simple a group as the six permutations of three letters.

That,is the Rubik's cube.
This,quite surprisingly,is a joining line between thoughts and function,both of which still do have gaps we are not capable enough to know.In fact,Boolean algebras,which deal with simply different aspects of one type of structure are a part of abstract algebra,which involves Algebraic structures including groups, rings, fields, modules, vector spaces, lattices, and algebras. The term abstract algebra was coined in the early 20th century to distinguish this area of study from the other parts of algebra.
One thing must be noticed here : perception.Now,this in case of all inventions,I think is the optimum plank of anything at all.Be it thoughts and be it subsequent development from or of further thoughts/innovations.
In cognitive psychology,perception involves both the physical senses (sight, smell, hearing, taste, touch, and proprioception) as well as the cognitive processes involved in interpreting those senses. Essentially, it is how people come to understand the world around them through interpretation of stimuli.Early psychologists like Edward B. Titchener began to work with perception in their structuralist approach to psychology. Structuralism dealt heavily with trying to reduce human thought (or "consciousness," as Titchener would have called it) into its most basic elements by gaining understanding of how an individual perceives particular stimuli.
Current perspectives on perception within cognitive psychology tend to focus on particular ways in which the human mind interprets stimuli from the senses and how these interpretations affect behavior. An example of the way in which modern psychologists approach the study of perception is the research being done at the Center for Ecological Study of Perception and Action at the University of Connecticut (CESPA). One study at CESPA concerns ways in which individuals perceive their physical environment and how that influences their navigation through that environment.
Again,thought which is a part of perception refers to the ideas or arrangements of ideas that result from thinking, the act of producing thoughts, or the process of producing thoughts. Although thought is a fundamental human activity familiar to everyone, there is no generally accepted agreement as to what thought is or how it is created. Somehow, thoughts arise in the mind from the product of subconscious brain processing.
Mathematical psychology is an approach to psychological research that is based on mathematical modeling of perceptual, cognitive and motor processes, and on the establishment of law-like rules that relate quantifiable stimulus characteristics with quantifiable behavior. The mathematical approach is used with the goal of deriving hypotheses that are more exact and thus yield stricter empirical validations. Quantifiable behavior is in practice often constituted by task performance.

As quantification of behavior is fundamental in this endeavor, the theory of measurement is a central topic in mathematical psychology. Mathematical psychology is therefore closely related to psychometrics. However, where psychometrics is concerned with individual differences (or population structure) in mostly static variables, mathematical psychology focuses on process models of perceptual, cognitive and motor processes as inferred from the 'average individual'. Furthermore, where psychometrics investigates the stochastic dependence structure between variables as observed in the population, mathematical psychology almost exclusively focuses on the modeling of data obtained from experimental paradigms and is therefore even more closely related to experimental psychology/cognitive psychology/psychonomics. Like computational neuroscience and econometrics, mathematical psychology theory often uses statistical optimality as a guiding principle, assuming that the human brain has evolved to solve problems in an optimized way. Central themes from cognitive psychology; limited vs. unlimited processing capacity, serial vs. parallel processing, etc., and their implications, are central in rigorous analysis in mathematical psychology and all that is compilation itself is a part of everything but also,very much,of philosophy.
Bibliography
3. http://staffhome.ecm.uwa.edu.au/~00021149/Academy/2011/boolean.pdf
4 .https://en.wikipedia.org/wiki/Boolean_algebra
5. http://www-history.mcs.st-and.ac.uk/HistTopics/Beginnings_of_set_theory.html
6. http://www.math.umt.edu/tmme/monograph2/lynenglish_article2.pdf
4 .https://en.wikipedia.org/wiki/Boolean_algebra
5. http://www-history.mcs.st-and.ac.uk/HistTopics/Beginnings_of_set_theory.html
6. http://www.math.umt.edu/tmme/monograph2/lynenglish_article2.pdf
7. https://en.wikipedia.org/wiki/Ada_Lovelace
8. https://en.wikipedia.org/wiki/Abstract_algebra
9. http://plato.stanford.edu/entries/algebra/
10. https://en.wikipedia.org/wiki/George_Boole
11. https://en.wikipedia.org/wiki/Cognitive_psychology
12. https://en.wikipedia.org/wiki/Mathematical_psychology
8. https://en.wikipedia.org/wiki/Abstract_algebra
9. http://plato.stanford.edu/entries/algebra/
10. https://en.wikipedia.org/wiki/George_Boole
11. https://en.wikipedia.org/wiki/Cognitive_psychology
12. https://en.wikipedia.org/wiki/Mathematical_psychology








0 Comments
What are your perspectives?